波恩哈德·黎曼:数学的先知与科学的奠基者
# 波恩哈德·黎曼:数学的先知与科学的奠基者
## 引言
波恩哈德·黎曼(Georg Friedrich Bernhard Riemann,1826年9月17日-1866年7月20日)是19世纪德国的一位杰出数学家,他的研究在数学分析、微分几何和数论等领域产生了深远的影响。黎曼不仅开创了黎曼几何,为后来的爱因斯坦的广义相对论提供了数学基础,还在复分析和数论方面做出了重要贡献。本文将全面探讨黎曼的生平、主要成就及其对后世的影响。

## 一、生平与教育
### 1. 早年生活
黎曼出生于德国汉诺威附近的一个小村庄,他的父亲是一名牧师,家庭条件虽然并不富裕,但却十分重视教育。黎曼从小展现出卓越的数学才能,尤其在几何和代数方面表现出色。1834年,他进入了当地的学校,1840年,黎曼进入了哥廷根大学,师从著名数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss)。
### 2. 学术生涯
在哥廷根大学,黎曼的才华得到了充分的发挥。他不仅学习了数学,还对物理学和哲学产生了浓厚的兴趣。1847年,黎曼获得了博士学位,他的论文探讨了复变函数的性质。在高斯的支持下,黎曼逐渐在数学界崭露头角。
1851年,黎曼成为了哥廷根大学的讲师,随后在1857年被任命为教授。他的职业生涯虽然短暂,但在这段时间内,他发表了多篇具有重要影响的论文,奠定了他在数学界的地位。
## 二、主要成就
### 1. 黎曼几何
黎曼最重要的贡献之一是开创了黎曼几何,这是一种研究曲面和多维空间的几何学。1854年,黎曼在他的著名演讲《关于假设的基础》中首次系统性地提出了黎曼几何的基本概念。
#### (1)曲率与测地线
黎曼几何的核心思想是研究曲面的性质,特别是曲率的概念。黎曼引入了测地线的概念,这是一种在曲面上最短的路径。通过测地线,黎曼能够描述在曲面上运动的物体的轨迹,这一思想为后来的广义相对论奠定了基础。
在黎曼几何中,曲率是描述空间几何性质的关键参数。黎曼通过定义不同类型的曲率,使得数学家们能够更好地理解复杂的几何结构。例如,正曲率表示空间向外凸出,负曲率则表示空间向内凹陷。
#### (2)多维空间的概念
黎曼的几何学不仅限于二维曲面,他进一步推广到多维空间的研究,提出了“黎曼流形”的概念。这一概念使得数学家们能够在更高维度上进行几何研究,极大地丰富了几何学的内涵。黎曼流形的引入为现代数学提供了新的视角,使得研究者能够探讨更复杂的几何和拓扑问题。
### 2. 数学分析与复分析
黎曼在数学分析和复分析方面的贡献同样不可忽视。他对积分理论的研究为后来的数学分析奠定了基础。
#### (1)黎曼积分
黎曼提出了黎曼积分的概念,这是对函数进行积分的一种方法。通过将函数的图形分割成小的矩形并求和,黎曼能够定义更为一般的积分。这一方法在后来的数学分析中被广泛应用,成为现代积分理论的重要基础。
黎曼积分的提出,使得数学家们能够更系统地研究函数的性质,特别是在连续性和可积性方面。黎曼积分的概念在后来被推广为更为一般的积分理论,如勒贝格积分,进一步丰富了数学分析的内容。
#### (2)复变函数的研究
黎曼在复变函数方面的研究同样具有重要意义。他提出了“黎曼面”的概念,这是研究复变函数的重要工具。黎曼面使得数学家能够更好地理解复变函数的性质,尤其是在多值函数的研究中,提供了清晰的几何视角。
黎曼面不仅为复分析提供了新的研究方法,还在物理学和工程学中得到了广泛应用。通过黎曼面的理论,研究者能够更好地理解复变函数在不同领域的应用。
### 3. 数论与黎曼猜想
黎曼在数论方面的贡献主要体现在他对素数分布的研究上。1859年,黎曼发表了关于素数分布的论文,提出了著名的“黎曼猜想”。
#### (1)黎曼猜想
黎曼猜想是数论中最重要的未解难题之一,涉及到黎曼ζ函数的零点分布。黎曼猜想认为,所有非平凡的零点都位于复平面上实部为1/2的直线上。这一猜想至今仍未被证明,吸引了无数数学家的关注。
黎曼猜想的提出,为数论的发展提供了重要的研究方向。许多数学家在黎曼的基础上,继续探索素数的性质和分布规律,推动了数论的深入发展。
#### (2)对素数分布的影响
黎曼的研究为后来的素数分布理论提供了重要的基础。他的工作不仅推动了数论的发展,也为后来的数学家提供了研究的方向。黎曼猜想的提出,使得许多数学家在探讨素数的性质时,能够以此为依据,进行深入的研究。

## 三、黎曼的数学思想
黎曼的数学思想具有鲜明的特点,尤其是在对几何和分析的深刻理解上。他的研究方法注重直观与抽象的结合,强调几何直观在数学研究中的重要性。
### 1. 几何直观与抽象思维的结合
黎曼强调几何直观在数学中的重要性,他认为几何图形能够帮助人们更好地理解抽象的数学概念。他的黎曼几何研究正是建立在对几何直观的深刻理解之上,使得复杂的数学问题变得更加清晰。
### 2. 系统化与严谨性
黎曼的研究注重系统化和严谨性,他在提出新理论时,总是能够给出清晰的定义和逻辑推理。这种严谨的研究态度对后来的数学家产生了深远的影响,成为现代数学研究的重要标准。
## 四、黎曼的影响与遗产
黎曼的研究对后来的数学家和科学家产生了深远的影响。他的理论和方法不仅推动了数学的发展,还为物理学、工程学等领域提供了重要的理论基础。
### 1. 对数学界的影响
黎曼的贡献在数学界得到了广泛认可,他的理论为后来的数学家提供了重要的研究方向。许多数学家在黎曼的基础上进一步发展了几何学、分析学和数论,使得这些领域得到了极大的丰富。
### 2. 对物理学的影响
黎曼几何为爱因斯坦的广义相对论提供了数学基础,爱因斯坦在建立广义相对论时,借鉴了黎曼的几何思想,特别是在描述时空的弯曲性方面。黎曼的工作使得物理学家能够更好地理解引力的本质,推动了现代物理学的发展。
### 3. 影响后世的数学家
许多后来的数学家,如希尔伯特、庞加莱和克莱因等,都受到黎曼思想的影响。他们在各自的研究中,继续探索黎曼提出的概念,推动了数学的进一步发展。

## 五、结论
波恩哈德·黎曼是一位杰出的数学家,他的贡献在数学和科学史上具有重要地位。他开创的黎曼几何不仅为数学提供了新的视角,也为物理学的发展奠定了基础。黎曼的研究方法、思维方式和理论体系对后来的学者产生了深远的影响,使他成为历史上最伟大的科学家之一。今天,我们仍然在他的理论和方法中汲取灵感,推动科学的不断发展。黎曼的名字将永远铭刻在科学史的丰碑上,激励着一代又一代的学者不断探索未知的领域。#历史不能忘记##草木中国历#
-
- 姜太公是否真的曾经用斗笠电鱼
-
2024-08-18 01:08:47
-

- 布金寺在古时候的哪个时期建成
-
2024-08-18 01:06:42
-

- 红颜薄命:探秘小乔与周瑜的佳话
-
2024-08-18 01:04:37
-
- 茜茜公主和罗密施奈德永远的茜茜公主
-
2024-08-18 01:02:32
-
- 孙子兵法作者是孙武还是孙膑 吴国孙武孙膑是孙武后人
-
2024-08-18 01:00:28
-

- 孔子与孟子:儒家学派的奠基者与继承者
-
2024-08-18 00:58:23
-

- 乐山大佛是空心的吗?乐山大佛不能拜的真相空心佛
-
2024-08-18 00:56:19
-

- 古时候天文学中,荧惑是指什么
-
2024-08-18 00:54:14
-

- 清朝狩猎场究竟是什么样的 这个地方 到底在哪里
-
2024-08-18 00:52:09
-

- 哈萨克斯坦国旗的历史演变是怎么样的?
-
2024-08-18 00:50:04
-
- 通天教主为什么同意封神榜计划?后来为什么又要阻止?历史
-
2024-08-17 17:51:05
-

- 秦始皇嬴政不立扶苏为太子的背后真相
-
2024-08-17 17:49:01
-
- 明朝第一硬汉:面不改色用碎碗片给自己割肉断筋
-
2024-08-17 17:46:56
-

- 明朝历史的独特之处在哪里?
-
2024-08-17 17:44:51
-

- 明清殉葬制度之异同,分别是什么样的?
-
2024-08-17 17:42:46
-

- 参拜舍利子祭赛国的舍利子是怎么拿回来的小白龙真的使
-
2024-08-17 17:40:41
-

- 耶律阮之死后的辽国皇位继承
-
2024-08-17 17:38:37
-

- 盘点二战时期参战国牺牲的最高将领
-
2024-08-17 17:36:32
-

- 傲视群雄的后梁,为什么被偏居一隅的河东灭亡?历史
-
2024-08-17 17:34:27
-

- 朱棣与永乐盛世:权力与繁荣的交织
-
2024-08-17 17:32:22



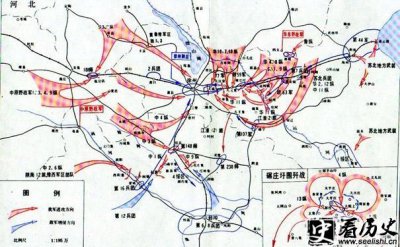 淮海战役第一阶段作战情况解析
淮海战役第一阶段作战情况解析 孙立人简介 孙立人夫人是谁 孙立人的子女后代
孙立人简介 孙立人夫人是谁 孙立人的子女后代 奥土战争背景具体是什么
奥土战争背景具体是什么 美国政治家约翰布朗个人资料介绍
美国政治家约翰布朗个人资料介绍 后人对幸田露伴评价怎么样
后人对幸田露伴评价怎么样 古罗马安东尼传奇故事怎么样的
古罗马安东尼传奇故事怎么样的 最低气温记录是多少度?在什么地方监测到的?
最低气温记录是多少度?在什么地方监测到的? 南朝宋临川王刘义庆是谁?人生是什么样的?
南朝宋临川王刘义庆是谁?人生是什么样的? 光武中兴期间刘秀采取的措施有哪些
光武中兴期间刘秀采取的措施有哪些 大武神王的儿子好童王子的事迹分享
大武神王的儿子好童王子的事迹分享